No. 13, Vol. 2. Vernal Equinox 2007
The Hieroglyphic Monad of John Dee
Theorems I-XVII: A Guide to the Outer Mysteries
by Teresa Burns and J. Alan Moore
John Dee’s Hieroglyphic Monad remains one of the most enigmatic works in the history of western Hermeticism. The best introduction still is C.H. Josten’s, which declares unequivocally that it is a work of alchemy, suggests many possible contexts, but adds that the “specific message which Dee tries to convey by his symbol of the Monad, and by his treatise thereon, is lost. His explanations are sometimes explicitly addresses to a mystae and initiati whose secrets we do not possess.”[1]
Composed by Dee in 12 days, the Monad was clearly accompanied by an oral teaching, and in his later writing Dee reminds the Court of his providing part of that instruction to Queen Elizabeth and perhaps, King Maximilian.[2] Dee himself called the Monad a magic parable, and for many years there was certainly a group of initiates that understood it well. Frances Yates has argued that the “more secret philosophy” behind the Rosicrucian manifestos “was the philosophy of John Dee, as summed up in his Monas Hieroglyphica.”[3] The Chymical Wedding of 1616, which Adam Mclean has noted is structured as an “elaborate Hermetic allegory” of inner transformation,[4] displays the Monad glyph prominently next to the first poem; Jacob Boehem’s 1625 Clavis and Ananasius Kirscher’s 1650 Obeliscus Pamphlicus also show this glyph and exhibit ideas strongly influenced by Dee’s work. The American alchemist and first governor of Connecticut, John Winthrop, used the Monad symbol as a bookmark, as did his son and grandson.
By the time 20th century scholars became interested in the Hieroglyphic Monad, those who understood the work seemed to have died with its secrets. The author of the first scholarly biography of Dee, Peter French, suggested that a major concern of Dee’s magical parable was the “Gnostic ascent to the One. . . The process of man’s spiritual transformation is therefore the deepest subject of this work, rather than the mundane alchemical quest for gold.”[5] Yet like C.H. Josten before him, and a series of commentators since, French felt that, “Dee wrote within an oral and secretive alchemical tradition that has probably been permanently lost.”[6]
Has it been? As the community of scholars and esotericists studying the Monad starts to overlap more each year, perhaps we have enough old information coming to light that we can resurrect this hidden teaching. Certainly at least part of the oral teaching has been hiding in plain site, within the very stream of the western mystery tradition that the Hieroglyphic Monad gave birth to.
We think that teaching can be recovered simply by looking at what contexts Dee wrote in and where parts of those contexts survive. Let us make the not-so-radical assumption that the work encodes many different levels of information at once, and describes many processes at once, and one of those is the process of initiation. Therefore the more one wants to understand the other processes, the more the student must actively participate in that initiatory process and discover the magical correspondences. Today, we have enough other works available to “rediscover,” on our own, what likely were two of the core oral teachings that accompanied the Hieroglyphic Monad: precessional astronomy and tantric gnosis.[7]
In fact, we contend that the process of carrying through a study of this work through to the point where a true understanding begins to enfold is in itself an initiatory process. Just as Renaissance actors used an elaborate three-dimensional mnemonic system to remember their lines, the student of the Monad needs to build up an at least three-dimensional, moving system of correspondences and how those correspondences transform into others, to start to understand the work.
Our goal in this commentary is to assist you on your own journey of discovery and apotheosis. This isn’t a cook-book guide. It’s a series of suggestions about how Monad might unpack through Theorem XVII, the Theorem which reprises the Sign of the Adept and so stands at the gate to most complex understanding of the Mysteries.
One of the secrets of that art known as physical alchemy known to the true initiate is that the Great Work cannot be achieved by physical, external, or mental means alone, but requires that in parallel to the physical processes of the alchemist’s laboratory and mental gyrations of the student’s mind a holistic inner alchemical transformation takes place within the entirety of the alchemist himself or herself. It is through the catalyst of inner transformation that the external process can be fulfilled. Thus also it could be said that the truest understanding of that which this work holds in potential or the truest understanding which lies latent with this corpus cannot blossom without similar inner transformative process in the mind and psyche of the student. The process by which this structure is built through the theorems presented, when accompanied by the proper focus and laid upon a firm, well-prepared foundation, is in itself an alchemical process in which the passages are contemplated and an understanding begins to dawn in the mind of the initiate.
Because of this, to read the Hieroglyphic Monad and not understand at first is to be expected; yet to read it with the wrong contexts is to invite misreading, confusion or the conclusion that the glyph really means nothing at all. For John Dee, to whom mathematics, magic, and divine cosmology were inextricably intertwined, any set of complex symbolic teachings would have to start with the same axioms and they would need to build consistently through all three fields. If we, as readers, start with different axioms, the transformation his work tries to trigger will never take place. For instance, if one searches through Dee’s lines and circles knowing nothing about geometry—or perhaps worse, thinking one knows, but superimposing a modern conception of math and numbers onto the ancient Greek perception, his geometry will make no sense, and one might simply conclude Dee didn’t understand numbers.
While we may discuss mathematical concepts in this guide, we want to do so within the western mystery tradition. If one knows nothing about that tradition--and many who have written on Dee have at best only a very superficial grasp of it--reading the Hieroglyphic Monad through Theorem XVII would be akin to reading through the Golden Dawn Outer Order rituals or worse, the cipher manuscript they came from,[8] and wondering why they make no sense. They do make sense if a person has the right context; they don’t if one doesn’t.
Theorem XVII and
the Analysis of the Key Word
To give an extended example of this, let’s look at one
place where we are certain part of Dee’s teaching has been transmitted,
in the Golden Dawn’s analysis of the keyword, an encapsulated ritual
utilized in the 5=6 initiation, the consecration of the Vault of the Adepti,
and in many shorter Adept-level rituals. Most notably, the INRI/LVX transformation
is part of what symbolically opens the Vault of Christian Rosenkreutz.
It has as its only known source the Hieroglyphic Monad, yet many
who are familiar with or participate in these ceremonies seem unaware
of this connection. Perhaps this is because one must understand the Monad
through Theorem XVII to really understand the keyword analysis, and the
few who study it in that much detail often lack the right contexts.
For the Adepti, we’ll start this commentary at Theorem XVII, then circle back to the frontispiece and opening theorems.
If one compares Theorem XVII and the Analysis of the Keyword, there at first seems little similarity:
| Theorem XVII | From the Golden Dawn Adeptus Minor Ritual | |
| As is evident from the sixth theorem, FOUR right angles can be considered to be in our CROSS, and the preceding theorem teaches that the sign of the QUINARY can be attributed to each one of them, the right angles of course being arranged in one way, but maintaining another position. The same theorem explains the production of the hieroglyphic symbols of the number FIFTY. Thus, it is very clear that the CROSS generally denotes the DENARY; and that in the order of the Latin alphabet, it is the twenty-first letter (whence it was the case that the wise ones called the Mecubalists signified the number twenty-one with the same letter); and finally, it can be considered very simply to be seen as one sign, no matter what kind of, and how much, other power it has. From all of these things together, we see it can be concluded by means of a very good cabbalistic explanation that our CROSS can signify to initiates, in a remarkably shortened way, the number TWO-HUNDRED-FIFTY-TWO. Namely, FOUR times FIVE, FOUR times FIFTY; TEN; TWENTY ONE; and ONE, add up to TWO-HUNDRED-FIFTY-TWO; which number we can deduce in still two other ways from our previous [statements]. Thus we recommend to cabbalistic Tyrians that they scrutinize this same [number], studying it in such a brief space, concluding the varied, skillful production of this Master Number to be worthy of the consideration of philosophers. I will not conceal from you here another memorable initiator to the mysteries. Our CROSS having suffered itself to be divided into two different letters, and as earlier we considered their [i.e. the letters’] numerical virtue in a certain way, we will now compare in turn THEIR VERBAL POWER WITH THAT CROSS, because from this may be born LUX (LIGHT), a WORD we perceive with the highest admiration, finally and magisterially (through the harmony and agreement of the TERNARY in the unity of the word). | Chief |
Let us analyze the Key Word. I. |
| All separate Wands and Cruces, and give Sign of Cross. | ||
All: Third All: |
The Sign of Osiris Slain. L - The Sign of the Mourning of Isis. V - The Sign of Typon and Apophis. (With head erect.) X - The Sign of Osiris Risen. (With head bowed.) L V X, (Lux) the Light of the Cross. (Saluting Sign and head bowed.) |
|
If one looks closer, and knows from earlier in the Monad that the “Cross” is X, the Quinary is Roman Numeral V, and Fifty in Roman numerals is L, we see Dee giving the LVX sign backwards.[9] Signing it backwards, just as an English or Latin writer would think of Hebrew as written “backwards,” or right-to-left, suggests a particular context. His use of the word “Mecubalist,” from Hebrew Mekubalim, suggests an even more particular context within Jewish mystical thought, just as his use of “Tyrian” near the end suggests a multitude of classical literary, Norse pagan, and Gnostic Christian contexts.[10] Those contexts, in different ways, suggest a four letter word turned into three; also, Theorem XIII (noting that 13 can become 1 + 3 or 4), as we’ll see later, could be interpreted as INRI. For a student of Dee’s, those meanings would already be part of the set of correspondences built up before getting to XVII, where INRI becomes LVX.
LVX, of course, is how the Latin word lux, or light, was spelled during the Renaissance. INRI is traditionally looked at as the initials of the Latin phrase placed by the Romans at the head of the cross on which Jesus was crucified, and stands for “Iesus Nazarenus Rex Iudaeorum,” or "Jesus of Nazareth, King of the Jews". Regardie points out that medieval alchemists suggested it meant “Igne Nitrum Renovatur Integra,” or “The whole of Nature is renewed by Fire,”[11] and indeed that could stand as a brief statement of one of the meanings of the entire Monad: the Sun and Moon as understood by previous theorems, plus the Cross of the Elements, are renewed by Fire as symbolized by the glyph of Aries.
Bridges and Weidner point out a more Rosicrucian version, “Isis Naturae Regina Ineffabalis,” or “Isis the Ineffable Queen of Nature.”[12] Noting the influence of the Monad upon Rosicrucianism, we might suspect this same interpretation could be found in this work. In fact, each of these interpretations can be equated to different levels of understanding the first 17 theorems, if one wants to look for them.
On the most basic level, the letters LVX are all parts of the cross:[13]
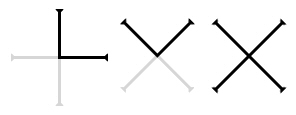
Dee equates light, and the LVX keyword as sign of the Adept, with the number 252, which by the end of Theorem XXIII of the Monad he will have equated with the philosopher’s stone, and with the sign of the Cross. He attributes the Cross to the “DENARY,” suggesting both the Pythagorean tetractys and the ten Sephiroth of the Tree of Life, and cryptically explains that this should be clear because the cross (X) is the 21st letter of the Latin alphabet. Some of the best Dee scholars and Judaic cabbalists have puzzled over this,[14] but the answer is clear if one understands Hermetic cabbala and geometry implied in previous theorems: INRI transforming to LVX would take place at the sixth Sephirah, Tiphareth, and if one takes the Sephiroth usually referred to Tiphareth (Yesod through Chesed) plus the “non-Sephirah” Da’at and connects them, one draws a hexagram or hexagon with Tiphareth in the middle. Similarly if one folds these into a cube, it has six faces. Noting the importance of all of these sixes, we observe: 1 + 2 + 3 + 4 + 5 + 6 = 21.
If one has built upon these geometries enough to see a 5:6 proportion developed throughout the preceding theorems, in particular in how the Pythagorean decad and Cabbalistic ten Sephiroth transform into systems based on twelve[15] (5:6 :: 10:12) one suspects 5=6 and the rank of an Adept carries additional significance that modern-day Adepts may have lost. The six-faced cube, incidentally, is one of five regular Platonic solids.
INRI turns into 252, and therefore the Cross, in yet another way, through a combination of Pythagorean mysticism and gematria. The gematria of I + N + R + I, yod nun resh yod, 10 + 50 + 200 + 10 yields 270, a rather significant precessional number. But if we remember that to the Pythagoreans, the Decad (10) was simply a higher form of the Monad, and we collapse this higher form into one unit, we have 1 + 50 + 200 + 1 = 252.
What else of the number 252? What are the two other things we should be able to “deduce” from his “previous statements”? Perhaps, as Josten noted, that 22 + 23 + 24 + 25 +2 6 + 27 = 252.[16] Secondly, it is the product of the three types of letters in the Hebrew alphabet: three mothers, seven doubles, and 12 simples, 3 x 7 x 12 = 252. Thus Dee equates the 252, the Light of the Cross, and the Philosopher’s Stone to the entire Hebrew alphabet, which of course to a Cabbalist signifies the entire represented powers of creation.
Then, Dee says “I will not conceal from you here another memorable initiator to the mysteries,” yet he seems to conceal it after all, telling is only that “Our CROSS having suffered itself to be divided into two different letters, and as earlier we considered their [i.e. the letters’] numerical virtue in a certain way numerical virtue in a certain way, we will now compare in turn THEIR VERBAL POWER WITH THAT CROSS, because from this may be born LUX (LIGHT), a WORD we perceive with the highest admiration, finally and masterfully (through the harmony and agreement of the TERNARY in the unity of the word).”
If the Adepti manipulate sections of the cross as we did with LVX, they may find two Hebrew letters whose sound, when put in the context of a particular stream of Greek alchemy, becomes I A O.[17]
Making the Key
Word Meaningful
While playing with letter and number combinations can be a lot of fun,
it won’t feel profound unless one understands the myriad of correspondences
that are supposed to be built into it. Thus we offer this guide to looking
at the frontispiece and first sixteen theorems.
While many of us fall into the habit of thinking we know much more now than those in days past, its crucial to understand that Dee’s hypothetical 15th century student would have had a much broader frame of reference, in terms of languages and allusions to classical literary and mathematical texts, than we have now. Dee himself had by far the largest library in England, and a study of what books he was collecting just prior to writing the Monad leads to interesting speculations.[18] We know he also was copying manuscripts he never recorded in his library lists, perhaps because the works themselves would have been too heretical.[19] We know he was fascinated by caballistic correspondences: though his only work on cabbala, Cabalae Hebraicae Compendiosa Tabella, has been lost, its title suggests it was something along the lines of Aleister Crowley and Allen Bennet’s “Sepher Sephiroth.” If something in the Hieroglyphic Monad seems like an allusion it probably is; if you see caballistic correspondences beyond the obvious, you’re certainly not imagining them.
As you study the Hieroglyphic Monad, you’ll notice that while the theorems in one sense build logically one to the next, in another way many of them ask the reader to cycle back through the whole group. Piece by piece, they build a structure which superficially has its representation in the glyph of the monad, but the body of knowledge represented by this work and indeed by the glyph itself is not to be understood by superficial information alone. As the glyph which embodies the core of the instruction to be had in this work is assembled piece by piece, so too is the inner teaching, the deeper mystery, which is to be found within this work, assembled in the mind of the initiate.
This guide will attempt to take you through in an accelerated form a few layers of the learning cycle which culminates in the keyword LVX. To attempt to fully unpack the wisdom available is far beyond the purview of this article and indeed were one to be thorough, it would fill volumes. Therefore in this article we will attempt to investigate but a few layers out of the many, and to help the reader to begin his or her own journey of discovery and transformation. In particular, we want to suggest the “building blocks” in the first ten theorems, and point to places in those which follow where one might be able to discern the references to the ancient Eleusianian or Samothracian mysteries, and references to precessional astrology.
The Frontispiece
Study the frontispiece, and note in particular the contexts Dee sets up
in it. The Monad appears in an egg between two pillars. Before
jumping to the egg in Theorem XVIII, just notice what is most obvious
visually: it is the “middle” between two pillars.

The odd statement on the garland suggests we must play with language as much as geometries (especially since Dee, in his letter to King Maximillian, asserts that Latin, Greek, and Hebrew alphabets each have significant geometries.)[20] The best way to render this line in English, “Mercury becomes parent and the king of all planets when perfected by stable, pointed Stilbon,”[21] helps most students’ understanding not at all unless the associations of Mercury and Stilbon are explored.
The odd language use suggests several contexts. As the notes in the
accompanying translation point out, Dee writes “![]() ”
in Greek, which must be transliterated to Roman letters to read Stilbon,
“shining one,” the god of the wandering star Hermaon or Mercury.
Yet, as the translators comment, “it also makes us think of Latin
stilus, which can refer to a stake, staff, or pale, a pointed implement
used for writing or for style in speaking. . . [r]ecall that Tehuti/Thoth
is often shown with a writing implement, and becomes the Greek Hermes/Mercury.
Thus Dee’s odd language nods to the Emerald Tablet of Hermes
Trismegistus as a governing context for the work.” It also suggests
a transformation between Mercury and the Sun which won’t become
clear until much later, because the usual “unperfected” understanding
would be that the Sun, not Mercury, is “Father” or “King.”
”
in Greek, which must be transliterated to Roman letters to read Stilbon,
“shining one,” the god of the wandering star Hermaon or Mercury.
Yet, as the translators comment, “it also makes us think of Latin
stilus, which can refer to a stake, staff, or pale, a pointed implement
used for writing or for style in speaking. . . [r]ecall that Tehuti/Thoth
is often shown with a writing implement, and becomes the Greek Hermes/Mercury.
Thus Dee’s odd language nods to the Emerald Tablet of Hermes
Trismegistus as a governing context for the work.” It also suggests
a transformation between Mercury and the Sun which won’t become
clear until much later, because the usual “unperfected” understanding
would be that the Sun, not Mercury, is “Father” or “King.”
While we don’t plan to refer to each note of the accompanying translation in this guide, we hope the brief analysis above does suggest to the reader one of the most important ways in to understanding the Monas: word-play. Dee was writing to someone who read not only Latin but Hebrew and ancient Greek, and further, was familiar with particular texts in those languages that have come to influence the core teachings of the western mystery tradition.[22] The best way to explore Dee’s language play is to attempt one’s own translation, but if that isn’t possible, the student has many resources available to at least explore word etymologies and which classical writers make frequent use of his terms.[23]
In Dee’s letter to Maximilliam, he refers to the Monad symbol
as “my London Seal of Hermes,”[24]
again suggesting the context of the Emerald Tablet. Further, he
expects his reader to know that the word monad, Latin monas
from Greek ![]() ,
(pronounced monas) means a unity, singularity, or point. This is
likely the “one” in the Emerald Tablet[25]
and certainly the basic unit (often directly translated as “monad”)
in Pythagorean, Platonic, and Euclidean thought. The fundamental unit
in Euclid’s Elements is the monad, and Euclid devotes all
of Book VII to exploring its meaning. Dee, of course, wrote the preface
to the first English translation of Elements, so one should become
familiar with that work, in its ancient rather than modern context. Geometric
images, to Euclideans and Pythagoreans, were sacred images and manipulating
them was a way to evoke the divine in one’s own mind.
,
(pronounced monas) means a unity, singularity, or point. This is
likely the “one” in the Emerald Tablet[25]
and certainly the basic unit (often directly translated as “monad”)
in Pythagorean, Platonic, and Euclidean thought. The fundamental unit
in Euclid’s Elements is the monad, and Euclid devotes all
of Book VII to exploring its meaning. Dee, of course, wrote the preface
to the first English translation of Elements, so one should become
familiar with that work, in its ancient rather than modern context. Geometric
images, to Euclideans and Pythagoreans, were sacred images and manipulating
them was a way to evoke the divine in one’s own mind.
The numbers 1, 2, 3 4; then 1 and 4, on the frontispiece likely both suggest the Pythagorean tetractys, which will be referred to indirectly in many theorems.
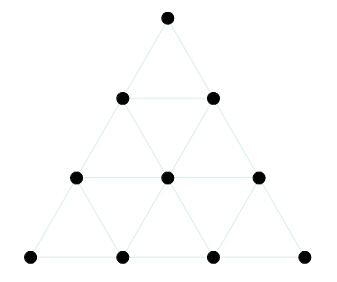
The Tetractys
The bottom line of a tetractys add up to 10, 1+2+3+4=10, just as there are ten points; the top point, 10 or the Decad, is simply a higher order Monad. The irregular spacing of these numbers on the frontispiece has made some suspect a cryptogram,[26] if so, we’d suggest that the cryptogram is simply “LVX” written in yet another way. Note that both the ten points of tetractys and the sum of its first line make 10, X; 1 and 4, as 1 + 4 = 5, to V, and both together (10 x 5) to 50, or L. We have LVX again, backwards.
At the bottom of the frontispiece, we find a quote from Genesis, part of the ten-fold blessing of Isaac to his duplicitous son Jacob. Thus yet another context is suggested; knowing Dee’s other interests, we might be much more successful looking for Gnostic or caballistic explanations of passages in Genesis rather than mainstream Christian ones.
Many have noticed that the Monas glyph appears on both versions of Dee’s Propaedeumata aphoristica. Dee wrote the first version as part of a letter to Gerard Mercator in 1558; his revised edition was published in London in 1567. It is available in an excellent English translation by Wayne Shumaker which includes, from a history of science rather than Hermetic perspective, analyses of Dee as a mathemetician, and the aphorisms as understood through the lenses of applied mathematics, physics, geocentric astronomy, and astrology. We hope someday someone who understands the Monad through the lens of Hermeticism well enough to explicate all 24 theorems will have the time to back through these 120 aphorisms and add to Shumaker’s commentary.
Theorems I-III
and I-X
Given the contexts set up on the frontispiece, we might
expect to find references to the Pythagorean tetractys, especially since
one explanation of that sacred figure is that the first row represents
zero dimensions (a point); the second, one dimension (a line segment running
from the first point to the second), the third, two dimensions (a plane,
defined by a triangle or three points and sharing the same shape as the
tetractys in 2D); and the fourth, three dimensions (a tetrahedron, defined
by four points and sharing the same shape as the tetractys in 3D). We
might also expect to find references to the cabbalistic Tree of ten Sephiroth;
we might expect references to Genesis, and we would certainly expect references
to the Emerald Tablet.
I.
To fully comprehend the ideas in this group of theorems, and indeed the
whole Monas, one must constantly cycle back through, so that later
understandings also change how one understands what is read before. Theorem
I, therefore, starts with what we are able to see: a line and a circle,
or the first two dimensions and how they create the third. We don’t
“see” a point, so we can’t start with it.
II.
Here Dee introduces the idea of a point, and in doing so invites us to
cycle back through Theorem I. He equates it to a point of light, or a
spark of consciousness. If we think of many of his theorems as energy
transformations, here we also have the idea of energy that has been localized,
and is no longer a stream or ray, and he would find support in the modern
notion that the tiniest quantum particles are energy that is vibrating
in one place and not streaming in motion.
Macrocosmically, the monad, the beginning point for manifestation, is light localized to a point. It takes on dimensionality by becoming a stream, or an infinite flow of points, thus giving us a line (first dimension). An infinite flow of lines give us a plane, or the second dimension. The circle, the most “perfect” figure in plane geometry, can’t be defined without either. So far, Dee’s explication could be straight out of Euclid, though one may cycle back for other interpretations later on.
III.
Now the two-dimensional “circle’ becomes a sphere, and so
the Earth. Dee’s “light” alludes to the fiat lux
of Genesis and thus the creation of all things from light. One might want
to further explore the different meanings of “circle” and
“sphere” to ancient writers, for they carry layers of significance
lost in our modern notion of these as “only” geometric objects.
At the very least, “circle” and “sphere” both
involve movement and an unending, usually sacred, cycle.
Because this theorem says that this middle point can also represent the earth, Dee is making the point or monad the top of the tetractys or decad, and further suggesting that the “Earth,” composed of the monad/decad, is referred to the tenth Sephirah, Malkuth.
As he is introducing the idea of the Sun, Moon, and other Planets completing their paths around the earth, Dee seems to be suggesting a geocentric view of the universe, and indeed, many very good writers have assumed, from this Theorem and XVIII, that this was his view. They neglect to note what should be obvious to Hermeticists: that if “I” am the spark of consciousness, that spark will be the center. Similarly, those of us who study astrology today do not think the Sun revolves around the Earth, but we know we have more accurate charts when we know the exact location on Earth to draw the chart from. “Earth,” or a point on Earth, is the frame of reference, the point from which other phenomena are observed and upon which other forces act.
It is very important to keep this idea in mind when working through the later Theorems, especially if you try to project these concepts onto the Tree of Life, or that Tree onto a Sphere. You are not attempting a diagram of the solar system; you are attempting a diagram of how consciousness comes into manifestation.
It his later theorems and in the Propaedeumata aphoristica, Dee will want us to understand that cosmic forces influence us in the same proportions that they stand in relation to us, that we can observe from our central “point.” We do not observe from the point of reference of the Sun, but from wherever we are on earth. We are analyzing our own being and consciousness from the geometries we reflect from our vantage point on Earth.
Finally, note that here and in most places Dee capitalizes SUN and MOON, which throughout also refer to the marriage of Sun and Moon in the Emerald Tablet.
IV
This theorem starts to test our ability to visualize the Monad in three
dimensions and rotate it around so it is viewed from different perspectives.
The moon would “appear” to be superior from the point of the
observer: it is placed there not because it is superior, but because
it looks that way from Earth. It “appears to the ordinary
person” that the Moon emulates the size of the Sun because the Full
Moon looks the same size as the Sun.
Yet the face, or semi-sphere, always reflects the light of the Sun—it does not generate light.
The next lines, that the Moon desires to be impregnated by the Sun, should be cycled back to when one has a greater understanding of what “Sun” and “Moon” may mean in the Emerald Tablet, but on the most simple level we have a description of the phases of the Moon: saying it desires to be impregnated (in appearance) by the light of the Sun means it wants to become full and look like the Sun.
Of note, the Moon in Dee’s Monad looks like Diana’s Bow, the first phase of the Moon after it has conjuncted the Sun and disappeared (the New Moon), then reappeared as a tiny sliver in the sky.
V
Note that this Theorem, V, refers to light, the essential element of alchemy.
The capitalized “LVX” for “light” in the Latin
original of Theorem V also implicitly refers us to the LVX analysis in
Theorem XVII, or begins an idea that the later Theorem completes.
Five also refers us to Venus and the Pentagram, which is formed in the sky if one watches solar conjunctions of Venus and the Sun from the Earth.
Finally, by equating the creation of the first day and night with the “LVX” of the philosophers, Dee implies that alchemy involves the measurement of time and space, and so introduces the idea of precessional astronomy. Cabbalists and fundamentalists have argued about the meaning of the Hebrew word for “day,” the former arguing that that this word meant not our current conception of day, but a unit measurement of time: a day, week, era, age. Following this interpretation, we should look at numbers in terms of spatial and temporal unit measures.
VI
As V refers to the Pentagram and Venus, VI will refer to the Hexagram
and Mercury, as the pattern of conjunctions between Mercury and the Sun,
viewed from earth, form a Hexagram.
In certain ways the first ten Theorems can be referred to the Sephiroth and their places on the Tree,[27] but notice this isn’t apparent until VI, which would correspond to the sixth Sephirah, Tiphareth. This is important because it again suggests our frame of reference.
Tiphareth represents the highest level of manifestation that we can perceive from our own consciousness. The light of Kether reaches us through Tiphareth, which is why it is often referred to the Sun. We can’t see the center of the galaxy, but we can see the Sun, even though all the power that the Sun wields comes from the center of the galaxy. We can understand what we can’t see, but first have to understand what we can see. So in one sense Theorem I starts with what we can see, but in another, Theorems I-V are all the abstractions you have to set things up until you get to what you can really see. So we know that the “Sun” and “Moon” in first 5 theorems will likely be concepts we’ll later return to, with new definitions.
For instance, we know the “one thing” or monad of the Emerald Tablet has the Sun as its Father and Moon as its mother; or is the product of the marriage of the Sun and Moon. This Theorem, referring as it does to the Sun and the Moon and a uniting point, suggests at least one type of union at Tiphareth.
In this context, the reference to “body, mind, and soul,” directs us to the nephesch, ruach and neschamah, the three parts of the soul to cabbalists. One is invited to meditate further upon what, beyond 3 + 4 = 7, Dee means when he tells us that the septenary manifests from the ternary and quaternary. Remember that “seven” was the usual count of both planets and alchemical metals.
Dee’s comment about the octad won’t make sense until one has built a structure beyond Theorem XVII, but his suggestion, in the context of precessional astronomy, may be that the ancient Magi had never observed something in the sky, even though they may have calculated it.
VII
At first this Theorem seems like a reprise of what has come before. The
four lines and the language of “flowing” might remind us of
the four rivers of Eden in their esoteric or cabbalistic context. But
very subtly, Dee is returning to the idea of the pentagram: by displacing
the central point from the cross, we now have five. This central point,
recall, was the point of origin from which the line and plane was formed,
and in effect governs the four elements as Dee has equated them to the
lines. Because all four elements flow out of the original creative light,
and because the displaced central point gives us the fifth point, we can
infer a pentagram with the crowning point of Spirit, which then governs
the four elements.
VIII
We have another reference to the tetractys in theorem 8, whose number
refers us also to the octad or octave. The Pythagoreans had both a tetractys
of addition, which Dee refers to directly by again noting a connection
to the denary (1+2+3+4=10), and a more complex tetractys of multiplication,[28]
whereon the fourth level, referred to the third dimension, contains the
first two cubic number: 2 x 2 x 2 and 3 x 3 x 3. The first of these, 23,
equals 8.
X, the 21st (3 x 7) letter of the Roman alphabet, gives us another of the letters in our keyword.
IX
The double reference to the SUN and MOON return us to the Emerald Tablet
and the one, or monad, having the Sun as its father and Moon as its mother.
Dee suggests we see the “Sun” and “Moon” both
as circles which conjunct the cross; if we expand from two dimensions
to three, we have two spheres.
Nine also refers us to the ninth Sephirah, Yesod, associated with generation, and the synthesis of the influences of all the other Sephiroth. It constitutes the “foundation,” or formative blueprint, for the manifest world in Malkuth. Note that Theorems 6, 9, and 10 refer directly to Sephiroth as usually numbered, which the other theorems in 1-10 do not, perhaps because the 6th, 9th, and 10th Sephiroth are on the Middle Pillar.
If we start to conceptualize a three-dimensional Great Tree from the information presented thus far, we have two spheres, the Sun and the Moon, with the axis of the Middle Pillar running through their central points, conjuncting the cross.
X
This theorem sets up the 10:12 or 5:6 ratio explicitly in the first line,
by using the odd Latin Dodecatemorii instead of the more usual
zodiacus. It likely refers us to works on the geometric solid dodecahedron
as well as the zodiac; thus time and space measures continue to coincide
and the unit numbers significant to one are significant to the other.
This word and number play invites us to consider how spatial and temporal
units of twelve divide and govern our understanding of the 10th Sephirah,
Malkuth, the manifest Kingdom.
Within this manifestation, fire is the penetrating, fructifying, purifying force. Dee’s wordplay further equates fire with Hermes[29] and the symbol for Aries, the first sign of the zodiac. Dee makes it clear he is using the sign for Aries, rather than “Aries” itself, in any of its many references.
Theorems XI-XVI
From this point on, our guide can only be as clear as your
understanding of the first ten theorems. Wherever Dee’s meaning
is not clear, we again suggest looking at his wordplay, cycling back through
the earlier theorems, and trying to visualize in three dimensions what
he is talking about.
XI
When Dee speaks of “the time of 24 hours, in the mode of the equinox,”
he again suggests numbers that are temporal unit measures and so alludes
to the precession of the equinoxes.[30] The
“most secret proportions” of “our” earth are these
precessional numbers. Note also that the Monad has 24 Theorems.
Eleven also refers to the “non-Sephirah,” Da’at or Knowledge. Sometimes Da’at is numbered only when Kether is not, suggesting it is the faculty by which we experience gnosis of all we can’t see, and that mystical state by which an individual experiences the unity of all of the Sephiroth.
From this point of Gnosis, one can now conceptualize a Great Tree whose “axis” runs from Kether to Malkuth, and whose proportions are precessional numbers. At Malkuth, it must intersect with the Cross of the Elements, which again divides time and space in terms of precessional numbers: four directions, four seasons; and so on.
XII
In this Theorem and the one which follows, Dee’s language use and
literary allusion become particularly dense.[31]
He creates a Latin word where he can find none that express his meaning,
and here and below, drops in a word from ancient Greek next to the Latin
Opus, or work, possibly suggesting the origins of his ideas in
Greek alchemy.
Dee provides glyphs of the planets and says they are all made from parts of the glyphs for Sun and Moon. Remembering our 10:12 proportion, and that Theorem X discussed mainly measures of 12, we might want to refer Theorem XII back to 10 and see what happens. If we have Great Tree of ten Sephiroth with the “Sun” and “Moon” as two spheres on the Middle Pillar, then all of the other planets, lying as they do “off” of the main axis, only exist as polarities or aspects of these energies.
His order of planets in this section has puzzled many, and should be returned to after one understands Theorem XVIII. They seem to correspond to the Four Elements, but only if we associate the fourth revolution with water; and could connect to the Four Ages of Lead, Tin, Gold, and Silver, but only if we somehow make the Moon and Mercury refer to Tiphareth or the Sun. The word “revolution” suggests temporal measurements, and indeed if one returns to these glyphs after further study, one may find that each corresponds to a type of temporal age, and the fifth figure--the synthesis of the preceding four—shows them combined into one zodiacal age.
If one considers the attributions of planets on the Middle Pillar, the progression from Saturn to the Moon is clearer. Saturn is usually referred to Binah, but can refer to all of the Three Supernals since it is the furthest “wandering star” we can see. Saturn/Binah’s reflection is to the Moon/Yesod, and what is “imprinted” in Yesod manifests in Malkuth, the physical world or Earth.
Here we also have “Mercury”/Hermes, the “pure magical spirit,” performing the “whitening,” one of the steps of physical alchemy, upon a zodiacal age, suggesting that external alchemy involves the transformation of time as well as space.
XIII
Dee’s language use in this theorem is so complex, and his transformations
between concepts so packed, that a reader really should go to the Latin
text to fully appreciate and understand it.[32]
As in the last theorem, he plays on multiple meanings of gnosis
and gnomon, and adds a play on multiple meanings of pyr,
fire, whose English cognates range from a funeral “pyre” to
a “pyr”amid. The idea of “fire” expressed through
the theorem is thus always alluding to a death and rebirth, hence the
association of this theorem to INRI.
Dee suggests that the Great Work is harder to do in this age than before, and seems to refer to the process of physical alchemy: the “soul” separated from the “body” on one level refers to the vapors given off as a substance is purified. But that interpretation alone won’t help us through the next paragraph. “SOUL” in this Theorem has two opposing meanings—the dross that needs to be burned off, and the gate to the inner mysteries.
Dee associates Lucifer, the “Light-bringer,” with Hermes/Mercury, the Microcosm, and the reborn Adam Kadmon. Seamlessly woven in as allusion to the witches Sabbath,[33] and thus perhaps the marriage of Lucifer and Diana, this Theorem suggests that for the INRI transformation to occur, the marriage of the Sun and Moon either transform or become analogous to the marriage of Lucifer/Hermes/Mercury to his sister Diana/Venus/the Moon.
What are we to make of this? How can Venus and the Moon refer to each other? Part of the solution lies outside of Theorems 1-17 of the Monas, in Dee’s idea of the Age of Venus and its Olympic Spirit Anael as Ruler of the Age.[34] If we assume that this was part of the oral teaching concerning precessional astronomy, “Venus” governs the Moon, and indeed the whole Middle Pillar, during the “Age of Venus.”[35]
We can more easily explain how Lucifer/Mercury/Hermes has, by means of this “SOUL,” been tied to the “MOON.” Consider that the “SOUL” (Latin anima) as vapors exuded during physical alchemy makes less sense that the more overtly sexual understanding we might draw from the Old Religion or Greek magical papyri. Soul, or anima, corresponds to ancient Greek psyche, which usually means mind, soul, or spirits of the dead, but in several passages of the magical papyri studied by Hans Betz, Betz concludes it means “the female pudendem; i.e. a synonym for physis,” and where it is translated as “soul,” it is frequently in an erotic context and suggests a double entendre on the other meaning,[36] just as “Fire-Being” in this same Theorem suggests a phallus.
If one is not familiar with Dee’s use of Olympic spirits, one might consider a common modern projection of the Venus glyphs onto the Tree, as a symbol encompassing all ten Sephiroth, representing the “Isis of Nature,”[37] and wonder if there is any connection back to this Theorem of Dee’s. If one sees in this brother-sister marriage an allusion to the legend of Isis and Osiris, one might see the outlines of how INRI stands for Isis Naturae Regina Ineffabalis,” or “Isis the Ineffable Queen of Nature.”
Finally, if returns to the usual reference of INRI, considers the Biblical crucifixion allegoricallym and remembers Jesus’s words-- “I am thirsty” --one might meditate upon two additional ideas: vinegar (as that given to Jesus on the Cross) as a solvent,[38] and needing water as an allegory for needing the Hebrew mother letter mem (water), or its several correspondences.
Dee concludes: “You see how exactly and openly the ANATOMY of our HIEROGLYPHIC MONAD corresponds to the SACRED MYSTERIES signified in both of these theorems (12 and 13).” We suggest that the sacred mysteries are precessional astronomy (in 12) and tantric gnosis (in 13).
XIV
Consider this theorem a reprise of the Emerald Tablet, with its
allusion to the “red earth” animated by the alchemists, as
a suggestion on how these two mysteries become one and the same. One might
also explore the multiple allusions made by the phrase “terra
lemnia.”[39]
XV
This Theorem opens with an allusion to the labors of Hercules, and indeed
one can spend many days connecting the labors to different alchemical
ideas. It also stacks multiple meanings of ram/Aries and bull/Taurus,
since the word for the animal, constellation, and zodiacal sign are the
same in Latin.[40] One should review the astrological meanings, and note that
because of the precession of the equinoxes, the constellations and signs
of the zodiac no longer match up; the vernal equinox is still called the
first point in Aries though it falls in Pisces. Approximately one zodiacal
age ago, in Roman times, they did match.
We suggest one look at this Theorem as another fusion of the mysteries presented in Theorems XII and XIII, which XV explicitly refers to.
Dee refers to the “hieroglyph” of Taurus in almost the same language as the Monad, and by studying the allusions and wordplay, one suspects it has little to do with the sign or constellation Taurus, and much to do with the mystery cults, or “houses,” which flourished during the Age of Taurus, approximately 5,000 years ago. This was the last age of the Great Goddess cultures in Europe and Mesopotamia, and the rise of the Old Kingdom in Egypt.
His wordplay reinforces the idea, including writing “Venus” in the genetive form, veneris, which carries several obvious puns in Latin: on veneror, worthy of respect or veneration, and as part of mons veneris, or the “mound of Venus.” Given the pun between mons and monad, we may be certain this latter meaning is among those Dee intended, and suggests wisdom attained through sacred sexual union; indeed the “union of Sun and Moon” referred to throughout must on one level refer to the hieros gamos. Further, the Taurus glyph, which looks like some of the line drawings of Cerrunos, Herne, and other Horned Gods of the Old Religion, is drawn with the circles slightly overlapping and so suggests one of the most sacred symbols to the Pythagoreans, the vesica piscis:[41]
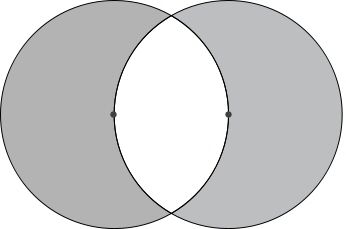
Dee’s quote (in ancient Greek) from Ostanes confirms this reading. Trying to trace who this ancient philosopher is and who quotes him should take the student to the heart of the three oldest alchemical manuscripts known in Dee’s time.[42] The complete saying, “Nature rejoices in nature, nature rules over nature, and nature is the triumph of nature” can be found in the story of Ostanes initiating Democritus into the mysteries, and points us towards a similar speech given by the angel Amnael to Isis: “Nature takes pleasure in Nature, Nature triumphs over Nature, Nature rules Nature. A human begets a human, the lion begets the lion, the dog begets the dog, grain begets grain: learn this from the farmer Achab. What is begotten against nature is a monster incapable of life. The Adepts teach this: only gold brings forth gold again at the harvest. This is the revealed mystery.”[43]
In this story, it appears Isis learns the secret of alchemy through ecstatic union with the divine, and, having become divine, passes that knowledge on to her son Horus. In the fragment, she is called not Queen nor Goddess but “Prophetess,” having become an oracle of the divine.[44]
To make sure the reader hasn’t missed his generative point, Dee puns on it yet again in the note at the end.[45]
XVI
When Dee tells us we must stop and philosophize a bit concerning the Cross,
he puns on “crux,” and means he will talk a bit about the
central point of the matter. What follows seems like a long discussion
of how to cut up the cross into different angles and make it correspond
to different letters, but if one looks closely, most of this section comes
right out of Euclid’s Elements and will parallel similar
ideas expressed in more detail in Dee’s Propaedeumata aphoristica.
In particular, he is telling us how to geometrically structure the ideas
he has presented in previous XV Theorems. As Turner and Burns discuss
in more detail in the notes to the accompanying translation,[46] Dee invites
us to visualize the cross in terms of conic sections.
First Dee asks us to picture a diagonal passing through a rectilinear cross; basically, a third line running through the point where these two intersect. His references to “V” and light also suggest the shape of a cone, if one imagine this in three dimensions. Then he tells us five (V) is a circular number, alluding to the circle as one of the four conic sections. If one makes the diagonal an axis for two cones sharing the same vertex, or point, and let that point be the intersection of the lines of the cross, we now have two cones and a plane. The plane can intersect the cones in one of seven ways, and makes one of seven figures: a circle, an ellipse, a parabola, a hyperbola, a point, a line, or a cross:
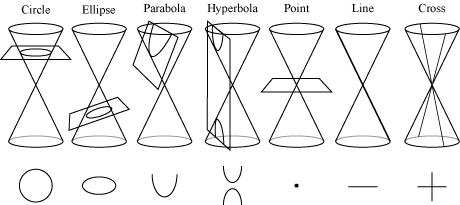
If the plane is running through the vertex, as Dee describes, then we can have only a point, line, or cross.
It is very important for the student to work through these images and draw them for herself, if one really intends to study the Monad in the context intended. If we use Euclidean geometry, the diagonal must be at a right angle, but we know Dee also had copies of the work of Apollonius of Perga,[47] and his understanding of conics in Propaedeumata aphoristica show he was extremely well-versed in these ideas.[48]
We also now have an image that Dee will use to express how a point of light, as the vertex of a cone, exerts influence. In his Propaedeumata aphoristica, particularly Theorems XXX through XLV, Dee will describe the properties of luminous cones, their axes, bases, and vertices, and strength upon the Earth at various distances, as a way of explaining how different celestial objects exert force upon the Earth. Recall that both versions of this work had the Monad glyph on their frontispiece, and Dee refers to these 120 aphorisms in his letter to Maximillian which accompanies the Hieroglyphic Monad.
The reference to “EL,” incidentally, is not only to the letter L or the Hebrew godname, but to an “l” in conics as defined in the Conica of Apollonius of Perga Book I, Proposition 11. The “l,” Latinized as latus rectum, is used in a particularly fascinating geometric transformation by which one derives a parabola from the conic section of an ellipse, and refers to a chord running perpendicular to the transverse axis and running through the foci. If such a notion seems absurd, consider how Dee likely influenced the first Latin translation of Conica.[49]
As one studies these ideas more, their connection to the ancient mysteries will start to take shape. For instance, one might study Appolinius of Perga’s references to the treatment of conic sections on the ancient Isle of Samos, study the geography of the Oros Fengari (Mt. Moon), and be surprised at the connections one can make.
Finally, one may also want to research any of the Renaissance contexts that viewed 1000 (103) as a perfect number. It was a common enough idea that it even lent mystical support to Elizabeth I’s regency, as her mother, Anne Bolyn, was Queen for 1000 days. Certainly, the end of this Theorem may be one of the reasons Elizabeth was so taken with Dee’s Hieroglyphic Monad.
How to Progress
Past Theorem XVII
Now we return again to where we began, the Theorem that gives
the LVX Sign of the Adept and the number, 252, which Dee refers to the
philosopher’s stone. Where does one go from here?
We have a few suggestions. We doubt one will be very successful in understanding what follows if one cannot geometrically visualize what has come before. If one can’t, it should be a clue to cycle back through the earlier theorems and slow down. Meditate upon them one by one.
Remember that geometry, music, art, architecture, and mysticism were not separate to the ancient Greeks, and Dee has absorbed their “monadic” view into his magic and alchemy. Apollonius of Perga wrote that, usefulness aside, the knowledge (gnosis) of different geometric propositions “are worthy of acceptance for the demonstrations themselves: indeed we accept many things in mathematics for this and no other reason.”[50] He and other Greek geometers worked out basic “scientific” and “mathematic” principles, but they never believed they were dealing with materiality only. They believed the world was formed by spiritual principles and the world of matter ultimately reflects something higher, intimately tied to gnosis and consciousness.
From this perspective, when you start explaining the origin of geometric shapes and forms, such as progressing from point to line to square to cube, you are both describing mystical principles of formation that exist in higher realms, but also, by describing them in a certain way, you are evoking those powers or principles in your own consciousness. The odd (to us) grammar used by Greek geometers makes this even clearer: propositions are introduced in a form called the perfect imperative passive, so instead of a sentence like “draw a line from the vertex at a right angle to the plane,” a literal translation would likely be, “let a line have been drawn from the vertex having a right angle where it has intersected the plane.” The effect of this type of writing is the implicit presence of what some translators have called “The Helping Hand, the well-known factotum in Greek geometry, who sees that lines be drawn, points be taken, perpendiculars dropped. No one who has read Euclid’s Elements in Greek will have missed it. . . The Helping Hand is always there to see that these things were done.”[51]
The form already exists, and by drawing it you are evoking it from within your own consciousness with the aid of this nameless “Helping Hand.” That’s why such mathematical principles often appear in the same context as the Hermetic maxim “as above, so below, as within, so without.”
We stress this because, if one wants to really understand the Hieroglyphic Monad, one must draw and meditate upon these images to evoke them in your own consciousness. Start with a point, a spark of light having location but no size. It does not exist in the world in its pure form, but it is part of everything that is form. The point is the basic building block of consciousness even though in and of itself it has no dimension. So to seek a true point, you must go into the realm of thought. As you contemplate this, what seems very simple becomes very profound. What things are dependent upon the formation of a point? This point is Dee’s Monad just as in another sense the Monad, or unit, is the entirety of the Great Tree. The Monad represents that ideal principle which cannot exist in its ideal form in matter, yet all of matter is dependent upon it.
From a point, move on to a line. From a line, move on to a circle. With these building blocks, move to three dimensions. Dee will introduce subjects to contemplate in every Theorem: by the time we start to meditate upon three dimensions, for instance, he’ll have referred us to the Tetractys; by Theorem V, the Pentagram as created by LVX; by VI, the Hexagram and Tiphareth, from which we can imagine a simple version of the Great Tree.
If we try to re-visualize this with the principles we ended Theorem XVII with, what would we have so far? We ideate a very far away “point,” the fiat lux of Genesis or the Limitless Light of cabbalists or the center of the galaxy to astronomers, as a vertex from which the light of all creation is emitted. Draw a line from that point to Earth; let the circumference of Earth define the circumference of our end of the cone.
Soon, on that same axis, the Middle Pillar, we will have two Spheres, the “Sun” and the “Moon,” and at the base of the cone, Malkuth, we have the “cross” from which we determine direction, which itself forms another sphere. We have a hexagram attributed to the “Sun,” which sometimes equates to Mercury/Hermes. We have a pentagram created by displacing the central point in the Cross of the Elements/Four Directions. For most of us, the Hexagram, the macrocosm, is easier to visualize in three dimensions (as two interpenetrating tetrahedra) than the microcosm. Can you see what a three-dimensional pentagram will look like?
With these ideas in mind, the student may want to cycle back through the entire first fifteen theorems and try to imagine, then draw, a 2-D representation of this three-dimensional tree. Dee has given you all of the proportions and magnitudes you need to do so. The point of discovery, where one has enough information to begin the architecture, is right at the end of this Theorem.
As you cycle through yet again, you may notice that all of the narrative allusions in the first ten Theorems are to creation stories; after Theorem II, the allusions and wordplay grow much more complex and seem to need a historical stream to fix them to. Why the allusions to the ancient city of Tyre, or the writings of Democritus, or indirectly, a Hebraicized fragment of an Isean story? Why mix all of the contexts?
Dee, we are certain, is drawing on the remnants he found in the Renaissance of a Theban magickal tradition from the third or fourth century A.D., and synthesizing it into his other ideas. While the manuscripts he had access to may not have dated before the tenth century, they draw on an older tradition, one we now have much more of a record of since the discovery and publication of Greek Magical papyri in different translations.[52]
One may want to look at later alchemical works like the Turba Philosophorum, but keep in mind that these writings, filtered as they are through at least two additional languages and cultures, may be less helpful in terms of what they say than in terms of what they point back to.
Finally, we would like to share with you the “Helping Hand” offered us by good friends with whom we have spent some time discussing the Hieroglyphic Monad:
Squaring the Circle in the
Creation of Sacred Space
This was how Bridges explained the geometries of the Great Tree to interested students back in 1991. As far as we know, he did not intend it as an explanation of the Hieroglyphic Monad. But if one visualizes this drawing of the Tree in three dimensions, one should see two spheres sharing the same axis, that axis ending at the center of a third sphere, at the center of a cross of four directions. One should see at least two cones.
If one locates where different Sephiroth are located and at the intersection of which curved or planar geometric boundaries, or puzzles over the “location” of different planets, you will indeed have a “Helping Hand” to go back through the geometries of the Hieroglyphic Monad, and proceed on the Theorem XVIII.
One Last Challenge
As the student, having mastered the material of the “Outer
Mysteries,” moves past the analysis of the keyword to Theorem XVIII,
he will encounter these illustrations:
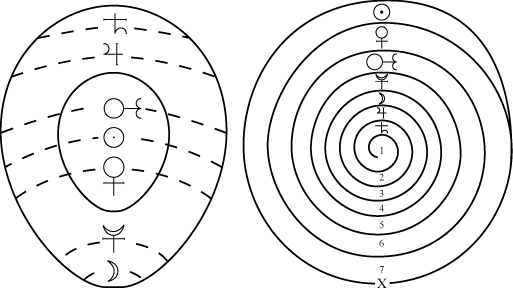
Can you explain them? We have found no satisfactory explanation in print, though we hope this article is in part a demonstration of how an oral teaching explaining the Hieroglyphic Monad either still exists or can be resurrected. The answer to this Theorem’s Sphinx-like riddle maybe found in part by looking at the other geometries in the Monas, in part by connecting them to related ideas in the Propaedeumata aphoristica, and in part by locating the images within Hermetic narratives.
The spiral, with Saturn (Lead) in the center and the Sun (Gold) on the periphery visually directs us to the alchemists Great Work of turning lead into gold, and indeed, as one studies this Theorem, one runs into some of the most common motifs of physical alchemy. But trying to derive a laboratory process from this Theorem will take one nowhere.
Neither will trying to explain the astronomy by only considering objects within our own solar system. Dee’s language near the end of this section—Helicis Revolutionibus—could easily be translated as heliacal revolutions, or revolutions around the sun, and so by the same logic some have used to suggest Theorem III shows a geocentric universe, one might say this Theorem shows a heliocentric, Copernican one.[53] We invite the reader to find a third alternative related to precessional astronomy and sacred geometry.
The INRI/LVX transformation should give us one clue to start: if the Outer mysteries of the Hieroglyphic Monad are encoded into this one transformation, at least part of the Inner Mysteries concern the projection of seven onto six: how to “map” the seven metals and planets of the alchemist onto a cube, thus moving our conceptualization into higher dimensional geometry.
But the easiest way to start into this Theorem is to look through the Corpus Hermeticum and Greek magical papyri for stories where similar images occur.
For instance, the first part of the Theorem, in its discussion of Ovi Metamorphosis (the metamorphosis or transformation of the egg), might direct us back to stories of Orpheus, whose musical magic, soul-travel, and journey through the underworld return us yet again to the ecstatic mystery cults of the ancient world. These stories present an entire narrative of cosmogenesis which includes the notion of time as the god that begat the world, and the universe itself as a cosmic egg. Yet the stories, to modern readers, seem to have as much to do with individual destiny as cosmological origins. We might also consider that the human aura has been seen for thousands of years as an egg-shaped energy field around the body.
Thus we start to see the outlines of the three-fold alchemical transformation of Hermes as the subject of the Inner Mystery: a cosmological unfolding of time and space, individual transformation and gnosis, and the ability, through the realization of the first and experience of the second, to aid in the perfecting of the consciousness of humanity.
Bibliography
Apollonius of Perga, Fried, MN, 2002, Conics, Book IV, 1st English edn, Green Lion Press, Santa Fe, NM.
Apollonius of Pergea, Densmore D, 1998, Conics, Books I-III, New rev. ed. / Green Lion Press, Santa Fe, NM.
Berthelot, M, 1887, Collection des anciens alchimistes grecs, G. Steinheil, Paris.
Betz, HD, 1986, The Greek Magical Papyri in Translation, Including the Demotic Spells, University of Chicago Press, Chicago, IL.
Bridges, V, 2003 (trans and commentary), “The Emerald Tablet,” in Wiedner, J & Bridges V, The mysteries of the great cross of Hendaye, Destiny Books, Rochester, VT.
Bridges, V & Burns, T 2007, “Olympic Spirits, the Cult of the Dark Goddess, and the Seal of Ameth.” Journal of the Western Mystery Tradition, vol. 2, no. 13, <http://www.jwmt.org/v2n13/book.html>.
Crane, G 1990s, The Perseus digital library, Tufts University, Classics Department, <http://bibpurl.oclc.org/web/2155>; <http://bibpurl.oclc.org/web/2155>; <http://www.perseus.tufts.edu http://medusa.perseus.tufts.edu/>.
Dee, J 1564, Monas Hieroglyphica, G. Silvius, Antwerp, <http://www.billheidrick.com/Orpd/Dee/JDMH.pdf>.
Dee, J 1564 (Latin), 1964 (English), CH Josten (trans and commentary),“A translation of John Dee’s Monas Hieroglyphica.” Ambix 12, 84-221.
Dee, J 2000, The Hieroglyphic Monad, JW Hamilton-Jones (trans and commentary), Samuel Weiser, York Beach, ME.
Dee, J, Turner, N, & Burns, T 2007, “A Translation of Theorems 1-17 of John Dee’s Hieroglyphic Monad,” Journal of the Western Mystery Tradition, vol. 2, no. 13, <http://www.jwmt.org/v2n13/partial.html>.
Dee, J, Shumaker, W & Heilbron, JL 1978, John Dee on Astronomy : 'Propaedeumata Aphoristica' (1558 and 1568), (Latin and English), University of California Press, Berkeley, CA.
Dee, J 1558, Propaedeumata aphoristica Ioannis Dee Londinensis, de praestantioribus quibusdam naturae virtutibus, ad Gerardum mercatorem rupelmundanum, mathematicu & philosophum insignem, London, England.
Euclid, Billingsley, H, & Dee, J 1570, The Elements of Geometrie of the Most Ancient Philosopher Euclide of Megara, Iohn Daye, London, England.
Euclid & Heath, TL 1956, The Thirteen Books of Euclid's Elements, Uniform Title: Elements, English, 2d ed., rev. with additions edn, Dover Publications, NY. Available on-line w/ minor edits by Joyce <http://aleph0.clarku.edu/~djoyce/java/elements/elements.html>.
Fried, M 2003,“The Use of Analogy in Book VII of Apollonius’ Conica” Science in Context, 16(3), Cambridge University Press, Cambridge, England.
French, PJ 1972, John Dee: the world of an Elizabethan magus, Routledge and K. Paul, London, England.
Josten, CH (trans and into) 1964,“A Translation of John Dee’s Monas Hieroglyphica.” Ambix 12, 84-221. Excerpt from introduction available: <http://www.esotericarchives.com/necronom/josten.htm>.
Klein, A 1982 (German) (preface, trans, and commentary), Die Monas-Hieroglyphe von John Dee aus London, Ansata-Verlag, Interlaken, Switzerland.
McLean, A 1984, (Commentary), The Chymical Wedding of Christian Rosenkreutz, Magnus Opus Hermetic Sourceworks, Edinburgh, Scotland.
Regardie, I, Monnastre, C & Weschcke, C 1989, The Golden Dawn : a complete course in practical ceremonial magic : the original account of the teachings, rites, and ceremonies of the Hermetic Order of the Golden Dawn (Stella Matutina), 6th ed., Rev. and enl. / complete index compiled by David Godwin ed., Llewellyn Publications, St. Paul, MN.
Roberts, RJ, Watson, AG 1990, John Dee's Library Catalogue, Bibliographical Society, London, England.
Rose, PL 1972, "Commandino, John Dee, and the De superficierum Divisionibus of Machometus Bagdedinus", Isis, vol. 63, no. 1, pp. 83-93.
Shumaker, W (trans and commentary) 1978, John Dee on Astronomy : 'Propaedeumata Aphoristica' (1558 and 1568), Latin and English, University of California Press, Berkeley CA.
Szonyi, GE 2001, "Ficino's Talismanic Magic and John Dee's Hieroglyphic Monad", Cauda Pavonis: Studies in Hermeticism, vol. 20, no. 1, pp. 1-11.
Taylor, FS 1930, "A Survey of Greek Alchemy", The Journal of Hellenic Studies, vol. 50, no. 1, pp. 109-139.
Tymme, T, Heninger 1963, A Light in Darkness, Which Illumineth for all the Monas Hieroglyphica of John Dee, Discovering Natures Closet and Cevealing the True Christian Secrets of Alchimy, Printed at the New Bodleian Library, Oxford, England.
Waite, AE 1973 (trans and commentary) The Turba Philosophorum. Samuel Weiser, Inc., NY.
Weidner, J & Bridges, V 2003, The Mysteries of the Great cross of Hendaye : Alchemy and the End of Time, Destiny Books, Rochester, VT.
Yates, FA 1972, The Rosicrucian Enlightenment, Routledge and Kegan Paul, London, England.
Notes
[4] McLean 1984, p. 1. McLeans’s structural analysis of the Chymical Wedding is by far the best available, and to us invites further comparison between that work and the Hieroglyphic Monad.
[7] We do not mean to imply that this entire teaching was part of the
gloss Dee seems to have provided to Maximillian and Elizabeth. Given the
apocalyptic concerns of heads of state at that time, and the interest
of many of them in prophecy, one might suspect his teaching to both concerned
precessional astronomy and what it may have predicted for their respective
reigns.
[8] Its worth noting that the cipher manuscript, written in the Trithemian cipher that was in Dee’s age a state secret, invites one to study how directly many of the ideas come from Dee’s magical circle as filtered through Rosicrucianism. For instance, the different projections of the Moon, Venus, and Mercury in the knowledge lectures connects almost directly to the Monas Hieroglyphica.
[9] For further explication, see Turner and Burns translation in this issue, notes 93-96.
[10] See Turner and Burns, n. 102.
[12] Weidner and Bridges, p. 319.
[13] Regardie points this out in his introduction to the second edition of The Golden Dawn, p. 13.
[14] See Turner and Burns, notes 99 and 100.
[16] Josten 1984, p. 175 n. 71.
[17] Thank you to Vincent Bridges for pointing this out to us.
[18] See Roberts & Watson 1990, pp. 3-19.
[19] See discussion in Bridges and Burns. Certainly, he had copied parts of alchemical manuscripts in Paris and Venice, and likely works of Cabbala of which we have no record.
[21] See Turner and Burns, translation and notes 7-10.
[22] Some would dispute that Dee had access to Hebrew texts beyond grammars and Biblical passages, but we think the evidence suggests otherwise. Dee visited most of the libraries in Europe which had Cabbalistic texts and he could read Hebrew; its inconceivable that he would not have read and copied some of them. Certainly he had access to, read, and copied parts of all three of the oldest extant alchemical manuscripts, two of which were in Paris and one in Venice.
[23] For instance, the Perseus Digital library at http://www.perseus.tufts.edu/ allows browsers to word-search through their entire Latin and Greek classical library, and their Latin and Greek dictionaries will return usage information along with entries. Sometimes this isn’t useful: for instance, learning that Dee uses the word “crux” or cross often, and so does the Vulgate Bible doesn’t particularly take us anywhere. But noting that Dee is occasionally using words in contexts similar to those Vitruvius in De Architectura might suggest an entirely new line of student.
[25] Turner and Burns, note 12.
[27] See http://www.jwmt.org/v2n12/appendix2.html.
[28] For a succinct explanation, see Donald Tyson’s Tetractys page at http://www.donaldtyson.com/tetract.html. Tyson also looks at a tetractys of Tetragrammaton.
[29] See Turner and Burns, notes 28-30.
[32] A Latin version is available on-line at: http://www.billheidrick.com/Orpd/Dee/JDMH.pdf. Also, Ibid. notes 42-55.
[33] See discussion in Bridges and Burns in this issue.
[38] For instance, consider this dialog in the Turba Philosophorum: “Frictes saith . . . ‘Oh how this nature changes body into spirit! Oh how admirable is Nature, how she presides over all, and overcomes all! Pythagoras saith: Name this Nature, O Frictes! And he: It is a very sharp vinegar, which makes gold into sheer spirit, without which vinegar, neither whiteness, nor blackness, nor redness, nor rust can be made” (Waite 1973, pp. 51-52).
[39] Turner and Burns, notes 56-58.
[40] Turner and Burns, notes 60-64.
[41] It suggests the same shape, though it is not exactly a vesica. If it were, the circumference of each circle would intersect the central point of the other.
[42] Taylor, in his survey of Greek alchemical texts, notes that the three earliest known manuscripts (as opposed to papyri) are Marcianus 299 in Venice (tenth or eleventh century;) Paris 2325 (thirteenth century) and Paris 2327 (fifteenth century.) Dee may have had access to all three; one wonders what papyri he, or the authors of these manuscripts, had access to. Taylor (1930, p. 113) says that the authors, as opposed to the copyists, of these alchemical texts wrote at dates no later “than the second half of the third century of the Christian era nor earlier than the first century” and include Democritus, Iamblichus, Ostanes, Cleopatra, Isis, Maria, and Hermes.” The names, obviously, are often pseudonyms.
[43] See Turner and Burns, n. 68. Waite gives a longer translation in his edition of the Turba Philosophorum: “When thou hast attained, my child, to the understanding of these things by way of a preliminary, consider creation and generation as a whole, and know that the man is able to bring forth man, the lion begets the lion, and the dog procreates the dog. Should it happen that a creature is produced that is contrary to nature, it is a monster which is engendered, and it hath no consistence. Nature charms nature, and nature triumphs through nature. The adepts having participated in the divine power, and having succeeded by the divine assistance, illuminated by the fruit of the prayers of Isis, made preparations with certain metallic minerals, without having recourse to other substances. Thus they succeeded by means of the substantial nature in triumphing over the matter employed in the preparations. In fact, even as I have previously said that wheat begets wheat and man sows man, so also gold serves for the increase of gold, and like things generally for the reproduction of their like. Now hath the mystery been revealed” (1973, pp. 22-23, 95.) Waite does not tell us what he is quoting from, but it appears he is paraphrasing Berthelot’s French translation of the ancient Greek given in Collection des anciens alchimistes grecs.
[44] Isis frequently is called the Patroness of magic, and this fragment echoes the more familiar story of her tricking Ra and learning the secrets of healing and eternal life.
[45] Turner and Burns, notes 65-75.
[47] Roberts & Watson note the history of the earliest version of Conica owned by Dee, now located in the Massachusetts library of Arthur Vershbow, who supplied these details: “The titlepage is inscribed ‘Joannes Deeus: Anglus: 1549’ and there are some Dee notes on the text. The front flyleaf has an extensive chronology of Greek scientists by Dee. The book also bears John Winthrop’s signature with the date 1631. Winthrop (1605-76) probably added Dee’s monad. The book belonged to other members of the Winthrop family. It is bound in calf with the small tool of the Habsburg eagle which appears on several of Dee’s Antwerp or Louvain acquisitions of this time” (1990, p. 82). We assume this is Books 1-IV in ancient Greek, as no Latin or English translations existed in Dee’s time, and Books V-VII have only been found in Arabic.
[48] Euclid’s actual treatise on conics has not survived, but part of the reason was that its ideas were completed and built upon by Apollonius of Perga, who is generally considered the greatest Greek thinker on the subject. For instance, Apollonius proved that all conics are sections of circular cones, and explored how to work with cones not produced by a right-angle, both of which seem key ideas in Dee’s use of conics in astronomy.
[49] Our term “parabola” comes from the Conica of Apollonius of Perga and was first used by Dee’s mathematical “son” Thomas Digges, with whom Dee was certainly sharing Federico Commandino’s 1566 Latin translation. Commandino may have shared an early version of his translation with Dee when the two met in Urbino the year before Dee’s publication of the Monas, and possibly Dee’s understanding of the Greek text he already had shaped Commandino’s interpretation. Dee and Commandino worked together to produce a Latin and Italian translation of the De superficierum Divisionibus of Machometus Bagdedinus (See Rose 1972), and the two men were clearly sharing manuscripts, with Dee as the teacher and Commandino as the student.
[51] Taisbak, qtd by Fried in the introduction to his translation of Apollonius’s Conica Book IV, p. xxix.
[52] For an excellent discussion of this tradition as a Greco-Egyptian-Hebraic synthesis, see Betz 1986, pp. xlii-xlvii. Of the mix of often incomprehensible languages in some of the papyri, he says, “Many of the texts depict the magician as a wondering craftsman who "seems keen to adopt and adapt every religious tradition that appeared useful to him" (p. xlvi). "This craftsman no longer understood the ancient languages, although he used remnants of them in transcriptions. He recited and used what must have at one time been metrically composed hymns, but he no longer recognized the meter". . . "For these magicians, there was no longer any cultural difference between the Egyptian and the Greek Gods, or between them and the Jewish God and the Jewish angels." (xlvi). Dee, as a scholar and linguist, clearly was trying to understand these ancient languages and re-synthesize the synthesis by understanding its geometries.
[53] The more usual line of thinking has been to equate the order of planets with an order of the spheres, thus using this Theorem for further evidence that Dee had a geocentric conception of the solar system.
[54] The references to Anaxagorus and Oedipus point us directly back
to this Theban current. Also, in the stories of Orpheus and the underworld,
we find our easiest connection to the “dark goddesses” of
the underworld so common in the Greek magickal papyri. See Betz 1986,
p. xlvi.