In Theorem I of the Monas Hieroglyphica John Dee sets the foundation for his work to depend upon the tools designated by the ancient Greek geometers as the valid method for solving problems considered to be worthy of mathematical investigation. These tools were simply the straight-edge and compass. Other tools became to be used in more practical problems in fields such as astronomy or navigation, but for the most philosophical speculations the mathematics involved was studied for its own sake, something now labeled pure mathematics. Dee considered these two tools more than objects for making designs on paper, but fundamental principles that governed the structure of the universe. In fact, throughout the Hieroglyphic Monad the explication reflects his esteem for the geometric principles of a God created universe.

He explains to the reader that it is through the line and the circle that "all things may be demonstrated" and therefore alludes to the actual straight-edge and compass method as the preferred method for demonstrating algebraic relationships. In Theorem II he is explicitly referring to Postulates I and III of Euclid Book I concerning the necessity of a point in the construction of a line and that of a line for the construction of the circle and therefore the point as the basis from which "all things commence to emerge in principle." Such a point is a Monad. Dee expects the reader to have awareness of this Greek geometry. That expectation implies an acquaintance with the three classical geometric problems: the squaring of the circle, the trisection of an angle, and the duplication of the cube. Without understanding that Dee expects his reader to be aware of these problems a large portion of the meaning of the Hieroglyph may be lost. The hypothesis set forth is that John Dee intended for the culmination to occur in Theorem XX by designating and thereby demonstrating a solution of the duplication of the cube. To affect this he embraces alternative methods employing the use of conic sections, acknowledging the non-existence of a classical solution, something that was only shown centuries later, and contrary to the contemporary attitude toward the quest for solutions. By considering these methods he is not accepting defeat; rather by so doing he utilizes geometrical concepts not in use until much later. This strongly suggests his awareness of geometry beyond the earthly three dimensions.

According to historian of science J. L. Heilbron, in the introduction to the translation of the Propaedeumata Aphoristica Dee really did have interest in the duplication problem, the construction of a cube with twice the volume of a given cube, for "there are two noteworthy points about Dee’s problems. First, they are inspired by the ancient, unresolved problems of squaring the circle and, above all the doubling of the cube."^[1] Second, the significance of the problem stems metaphysically from the story of a plague in Athens; after the oracle at Delos was consulted, in order to appease the sun god Apollo they were required to double the size of the cubical alter. Thus it is often referred to as the Delian problem.

For a thorough understanding of what John Dee was implying by the use of his Hieroglyphic Monad as an explanation of the duplication problem, and how it foreshadows the impossibility of construction of necessary points, including the ultimate transcendental nature of π, an investigation of the later development of algebra unto the nineteenth century becomes necessary. Maintaining consistency with the then current mode of thought that all problems have a solution he expresses this in Theorem I. However upon scrutiny he refers to the first and the most simple representations. In this way he relates unsolvability with complexity. Upon recognizing this he sets out to transcend with his geometrical demonstration of impossibility a concept with a long history of unnecessary and artificial restrictions, the straight-edge and compass. Only in twentieth century with the rather unexpected results of Kurt Gödel concerning undecidable logical sentences would the notions become to be clarified.^[2]

In the modern era when geometry is not emphasized in school such as it was in the era of the classical liberal arts, many students are usually not well versed in such ideas. But as any modern student of the occult will recognize, mathematics is clearly a requisite set forth by Agrippa in the 16th century in his Second Book of Occult Philosophy.^[3] Nevertheless, many today may be unfamiliar with these problems.

Posed in antiquity, these three problems remained unsolved until the inception of modern algebra in the nineteenth century. A related problem is that of the construction of an equiangular equilateral, or regular, polygon of an arbitrary number of sides. Constructions for these were known classically in several cases, yet it remained until 1801 for the theory behind which polygons were constructible and which were not to be resolved. This was accomplished by the great mathematician Carl Friedrich Gauss and published in his Disquisitiones arithmeticae. It had become clear that any number that was constructible was derived from a combination of the four elementary algebraic operations: addition, subtraction, multiplication, and division, and an additional more complex method, the extraction of the square root. Consequently to eventually understand these geometrical problems the theory of algebraic equations and the question of the solvability of equations by radicals was critical. The complete resolution of these classical problems only emerged when further considerations were made into the types of numbers that can arise as solutions to algebraic, or polynomial equations, at all.

A few years prior to the publication of the Monas, in 1545 Girolamo Cardano published his widely influential Ars Magna, or the Great Art. In it he presented general solutions for algebraic equations, most notably the solution of the general cubic and quartic equations, especially the most relevant one of "the cube and the first power equal to a number."^[4] In this work the demonstrations or proofs were almost entirely geometric. This is what Dee is referring to in Theorem I.

But it was indeed after Dee's publication, in the 1590's that the real advances in algebra took hold. Those were of a kind specifically dependent upon the introduction of new notations. The key figures, François Viète and Thomas Harriot were in mutual correspondence and Harriot himself gives much of the credit for his work to Viète. Dee and Harriot discussed mathematics and science in the early to mid 1590's while Viète had recently published his work in 1592. It is what transpired between the three of them that is unknown. Dee studied under Gerardus Mercator, the great navigator, and Harriot was also very proficient in the study of navigation. In fact Harriot, under the charge of Sir Walter Raleigh was instrumental in the survey of Virginia in 1585. While in Virginia Harriot translated the Algonquian language, and this work with linguistics played into his mathematical researches.^[5]

What Viète did was build upon the works of Cardano and the great Greek algebraist, Diophantus of Alexandria. He succeeded in developing a concept of species, that represented magnitude and thus could therefore use algebra to demonstrate, or solve, geometric problems. Dee did not have this insight. Viète being concerned with reconstructing the algebra of Diophantus was however limited in the perception of the necessity of homogeneity, or the idea that only quantities of like dimensions could be combined.^[6] Thus his challenge was to make sense of Cardano's cube and first power sum. He designated the series of gradations, the "first scalar magnitude is the side or the root" and then the square, the cube, the square-square, the square-cube, and so forth, to which corresponded the "magnitudes of comparison" or length (breadth), plane, solid, plano-plane, plano-solid, solid-solid, etc.^[7] This language was a perpetuation of the cossic system stemming from the introduction of algebra where originally the unknown was merely "thing" or "root" that later was rendered cosa in Italian. These terms were not even new with the Arabic for Diophantus also uses the "square-square" and as communicated by Psellus, the fifth power was actually considered by the latter Egyptians to be the "first undescribed" for beyond the fourth power nothing could be conceived. By insisting upon maintaining this homogeneity Viète was unable to allow for a generalization of dimension beyond four, though somehow there was this notion of plano-plane. It was indeed Harriot that succeeded in lifting this limitation that had its linguistic origins in this cossic system by letting a single fifth power be written as aaaaa.

Of course the familiar space of the world has three axes and for those in the time period three dimensions was the extent of spatial knowledge. Today the habit of referring to time as the fourth dimension is only correct in so far as 3+1=4; it is an additional dimension. Geometrically it is known that dimensions are defined by successive orthogonal, that is perpendicular directions. Thus when a cube is moved to a second location, the time elapsed has measured the displacement of the cube orthogonal to all of its three directions. But geometrically dimension and time are not related apart from the fact that time is a measure of one direction just as a meter is a measure of a single breadth of a three dimensional expanse. The analogy pertains to the difference between space and position compared with time and motion.^[8] Modern geometers have discovered many natural higher dimensional objects, in the sense of a certain simplicity, such as a cube or a circle that can be described as simple objects based upon a few fundamental relations. In particular, generalizations of cubes extend into higher dimensions, in the same way that polygons extend to polyhedra, or squares extend to cubes. As there are 5 Platonic solids and 4 stellated varieties there become 16 regular 4-dimensional hyper-solids, a trendy modern word, in contrast to archaic, 16 plano-planes. This cumbersome lack of language eventually just amounts to the use of n-volumes, where n designates dimensionality. Thus a 2-volume is an area. However polytope is usually used for higher dimensional regular objects.

For reasons not all too clear it is a fundamental fact of nature that there is something inherent about four that defined a limit to dimensional comprehension. The search for general methods of solving higher than fourth degree equations was also resisting success. This was resolved when Ruffini and independently Abel proved in 1799 and 1834 respectively, that the fifth degree equation was insolvable by radicals. This was taken further by Galois when he gave the complete characterization of solvability based on the concept of a mathematical group; where specifically the roots of the equation had to satisfy there own algebraic relations. The tragic life of Galois and the resistance to initial acceptance of his works is one of the great chapters in the history of mathematics.^[9]

Together what this did was illuminate the concept of algebraic numbers. Irrational numbers are of course those numbers that cannot be represented as a proportion between two integers. Thus any number that is an irreducible root, be it a square root, a cube root, or higher is irrational. Because the constructible numbers must obtain a maximum complexity of square roots they can potentially be irrational and not merely rational. When the analysis of the duplication of the cube is made it is seen to depend upon . Similarly the trisection of the angle depends upon a cubic equation and Pierre Wantzel in 1837 demonstrated these particular equations to fall beyond the constructible criteria.^[10]

But the squaring of the circle depends upon something more complex than these simple radicals. By setting the radius equal to 1 the area of the resulting square would imply that π is constructible number. As the investigations into the nature of π progressed it was soon suspected that it was not the solution of a quadratic, a cubic, nor a quartic equation, and in general, the solution of a polynomial of any degree. Such a number is a transcendental number, a number that is not the root of a polynomial equation with rational coefficients. This means that for whatever combination of powers with rational coefficients it can never equate to 0 upon the variable substitution of a transcendental number. On the other hand, for an infinite sum of powers, one can readily define series representations for numbers such as π that have a composition dependent only upon rational numbers, yet an infinite number (of them) are necessary. This may give an idea of the infinite or ineffable quality that can be perceived from a transcendental number. Yet many of the naturally occurring transcendentals appearing throughout mathematics consistently are defined in a like manner to the natural geometrical objects, i.e. through simple relations. Specifically with regard to π it is the ratio of the circumference to the diameter of a circle. It actually is a fact that most all numbers are transcendental but not many are easily determined explicitly.

The idea for the proof of the transcendence of π through the use of the method of continued fractions is essentially due to Johann Lambert; however he only proved its irrationality in the year 1767. Earlier, Leonhard Euler proved the irrationality of e in 1737 but it was Joseph Liouville that in 1844 first proved the existence of transcendental numbers in his attempts to show the transcendence of e utilizing the method of introduced by Lambert. After Charles Hermite successfully proved the transcendence of e in 1873, building on a relation between e and π established by Euler, Ferdinand von Lindemann was able to extend the proof of the transcendence of e to that of π in 1882 ultimately proving the impossibility of squaring the circle.^[11]

Of course Dee could not expect his readership to understand the full implications of this, as he himself did not. He did understand, however that the manner in which the duplication of the cube was resolved classically, without the use of a straight-edge and compass not only could be, but was central to his comprehension of the Hieroglyph and that what is being expressed is the transcendental characteristic of God.

It is common knowledge that Apollonius of Perga was the key figure in the development of the conic sections, but one must also understand the history of how these geometric figures as described by Apollonius play a role in the context of Dee's developing awareness. Principally a conic section is the 2-dimensional curve that is formed when a cone is cut from various angles. The interest Dee seems to have concerns the circle, the horizontal section of a cone and a parabola, the open-ended vertical slice. The parabola can be algebraically described as having a focus a certain distance from the apex of the curve and a directrix parallel to the tangent of the apex that is the same distance to the apex as is the apex to the focus. Thus the distance of the perpendicular to the directrix through the focus is twice a fixed distance. The parabola is then described as the locus of points equidistant between the directrix and focus. Considering this it is surprising to find that the focus and directrix properties were not given in the Conics of Apollonius. The relationships are given by Pappus, but in historical context this work is not found in Dee’s library.^[12] That should not preclude the fact that Dee was unaware. Mathematical historian Julian Coolidge points out that after Pappus it was not until 1501 when a work by Giorgio Valla and another in 1522 by Johannes Werner reinvigorated the subject.^[13] Both of these works are cataloged in Dee’s library and the Werner tract was acquired fourteen years before the publication of the Monas.^[14] The work by Valla apparently summarizes the Greek works, including that of Pappus.

Hippocrates of Chios reduced the problem of duplication to one of constructing two mean proportionals. Menaechmus then successfully used conic sections, specifically parabolas, to construct the two mean proportionals and though not by straight-edge and compass, a solution to the duplication of the cube. Coolidge states it such that "if between two straight lines of which the greater is double the less it were discovered how to find two mean proportionals in continued proportion, the cube would be doubled."^[15] Indeed Werner described eleven methods for solutions to the Delian problem, including the intersection of two parabolas, one of two Menaechmus described. Since the mathematical analysis of the proportions reveals that constructed point must be determined by in order to effect this, take a parabola opening vertically defined as x²=ay. Then a second parabola opening horizontally is given by y²=2ax. The x -coordinate of the intersection is the length of the sought edge. A speculative account of how Menaechmus came to the solution by the intersection of two parabolas is given by Coolidge.

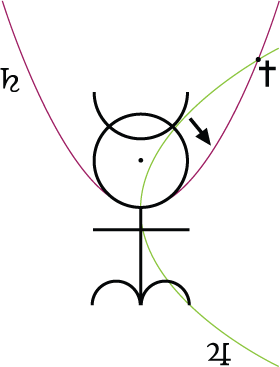With knowledge of this alternative solution to the duplication problem, upon a meditation of the Hieroglyph as a whole it will become apparent, most obviously, that the upper arc, the Luna glyph, is an idealized form of a parabola. This is demonstrated to the eye, because the horizontal line through the center forming the cross acts as the directrix. If this is true, one would then look for a corresponding point as the focus, and finding only the central solar point gives a clue to the fact that there should be a movement from above to below, elevating this solar focus, the Monad, to the lunar focus. This dynamic aspect of the geometrical construction has gone beyond simply lines and circles. Dee has now introduced conic sections, and with that quadratic equations, and a method of demonstrating a part of nature that is not dependent upon just line and circle. Now these objects become secondary and only relevant in the definition of a cone. The impression this leaves is that now Dee has created a 2-dimensional representation of a 3-dimensional process. Using this observation of the apparent existence of conic sections, specifically a single parabola, it is possible to critically examine his written explanations.

To analyze Theorem XX make note that the "adversary" is his counter-self, his devil’s advocate, and a necessary part of the demonstration. Following his thoughts, if the focus, in the sense of the conic were gone, if Christ were not of the cross the plane would cease to exist. Instead there would be two non-intersecting lines in space, one representing the body, or physical component, and the other the soul, representing the mental component, of a metaphysical material plane, consisting of physical, mental, and spiritual parts.^[16] The point, focus, or Christ would therefore be the spirit aspect. When this spiritual component does exist the two lines intersect to form a mathematically 2-dimensional plane. Understanding that this plane represents on one hand the Earth, apart from any alchemical connotation, then on a strictly physical level the earthly plane resides in the 3-dimensional world of experience. Metaphysically if the focus were not there the two lines could be mathematically existing in a 3-dimensional space, but having no connectivity they fail to define what then, with the spirit focus, is the ground of reality, existence. So together all three aspects, body, soul, and spirit represent three directions and thus an idealized cube, for even if that spirit focus in the final analysis is coplanar, its very say, prior existence within three dimensions, glues, so to speak, the earthly plane but does not eradicate the space in which the plane is embedded.

Especially note, that if the cross is the basic cross of the crucifixion then the horizontal identifies with the arms, the vertical, the legs, and Christ himself may be seen as the non-physical, non-mental, transcendent being. As such He projects orthogonally from the two dimensions into the world as a beacon of light, LVX. Of course, light may also be identified with the Sun which shines light from the heavenly realm onto the Earth and by extension the light of God, Christ, or simply LVX that shines into the world with a similar perspective. With the Sun represented as a circle having a definite center take note the placement of this symbol at the beginning of the Hieroglyphic Monad.

When he supposes that his adversary says of the point (focus) being apart from the Ternary he allows for the point to still exist, for without a point at all the foundations of Euclid’s geometry collapse as emphasized in Theorem II. Thus that point would be the point graphically within the solar component of the glyph however it could have various metaphysical interpretations when a complete alchemical contextual analysis is sought. Regardless, it must not cease to exist somewhere. Now, by Theorem X Dee explicitly implies that the Hieroglyphic Monad is not a static image when he refers to the necessity of "Aries to signify that in practice of this monad the use of fire is required." The use of the word Binary has several connotations, but principally the notion of the duplication process is usually to be inferred. He emphasizes that if the point were absent from the Binary, the Binary would cease to exist.

Notice also that if the point that defines the focus of a parabola ceased to exist so would the parabola. Therefore the glyph visually depicts the point and the arc above the horizontal indicating the representation of a parabolic figure with the horizontal of the cross corresponding with the directrix of the parabola, the solar point corresponding with the focus and the lunar arc idealizing the parabola. Since there is an action inherently implied, when he challenges his adversary to remove the point, the solar, mathematical focus of the parabola would in fact exist when the lunar component is moved downward, or what amounts to the same thing, the sun is exalted or elevated. Then this process represents the light coming to the Earth. But more than that the earthly material plane would only exist because of the intersecting of the Binary by the gluing of the focus.

By showing the necessity of the focus or in other words the necessity of the parabola this indicates that what he is referring to as the Binary, the conjunction of the body and soul, is actually the mathematical product in a literal mathematical sense. The intersection of two sets corresponds with multiplication while the union with addition. Thus it follows that the notion of Binary is also being used to indicate multiplication and in this case it must mean multiplication by two when considered in relation to the production of four, the Quaternary. Hence the proposition that at least in an active sense Dee is using Binary as a word for the duplication of the cube. Since the only known solutions at that time to this so-called Delian were problem through the use of conic sections and Dee is in particular using the solution by the intersection of two parabolas there must exist a second focus corresponding to an additional parabola. His transformation in Theorem XII reveals the orthogonal relation between and . Thus the second parabola being orthogonal to the first for the solution is naturally already present within the glyph. His notion of Quaternary is then indicative of the doubling of the Binary which is simultaneously symbolic of both the cubical space (because the spirit infused Binary is the principal for the earthly cube) and its duplication, the second cube with twice the volume of the original. Then the Binary as a supporting plane implies the Quaternary may then be identified with a plano-plane, or the duplicated cube. But also note that the word for square has long been associated with the Latin quadrus. This gives additional support to Binary being the multiplication by two to yield a cube of twice the volume.

By removing the point at the center of the cross there become four lines identified as the elements comprising a Quaternary, in the literal sense of a set of four objects. He challenges his adversary that regards the first Binary earthly cube to be the same as the Quaternary earthly cube, contends that a cube is a cube and any duplication only changes the scale of one and the same object. Thus the implication of the plano-plane becomes relevant and it is at this point the crucial observation is made. That is, this second cube, the Quaternary, is not merely a cube of a different size but that it is actually representative of the mathematical fourth dimension when Dee states that "the point must of necessity be present, because with the Binary it constitutes our Ternary, and there is nothing that can be substituted in its place." Then, acting as his own adversary, he sees that the hypothetically removed point must not just be present in his initial Binary defined Ternary, but because the final Quaternary is also a cube, it must have its own point that constitutes the Binary. Finally the way of the solution of the Delian problem is when the two parabolas intersect. So if the focus were necessary in both parabolas, call them and , then their intersection point, the solution, together with the fact that no other points were explained in this hieroglyph due to its fundamental and primary nature, implies all three points must actually be the same point. Therefore he must be saying only one thing, that the point identified as Christ in the initial stage prior to the action, in the final space acting as the bond must also be Christ and therefore it may be concluded that the final Quaternary is that world of the time of the Second Coming of Christ. Thus it is obvious why he was taking the trouble to illuminate the position of his "adversary" claiming that the two are merely scaled representations of the same thing, the earthly realm. He is rather pointing to the difference of this second space as being one where Christ has returned via the action of exaltation of the sun bringing forth the Light to the Earth.

According to Revelations^[17] it is prophesied that the Earth actually becomes the New Jerusalem. Yet when Dee concludes against his adversary because of his belief in the Second Coming and the New Jerusalem, the implication of a fundamentally different world, pointing out the impossibility of the two cubes being identical, he has still made it aware that the scaled cube is not just larger, but the fact of being larger on the one hand it would contain the initial cube and on the other hand by believing in the future prophesy of Revelations the two spaces are obviously separated by time. But his hieroglyph is showing that the two points and intersect and he is explaining the connectedness of the spaces. He has come to a contradiction that he can only resolve by understanding the time separation is not a separation at all but a connecting today called the fourth dimension.

To verify this to himself he would have to use his knowledge of the seeming intractability and probable impossibility of the classical construction problems in the manner in which they were first prescribed, using only straight-edge and compass. Since the problems are inherently 2-dimensional in nature he understands the difference between a plane and a space. He also knows that conic sections, while themselves planar, only come from a cone which resides in space. It would not be a leap to see that the cone represents the light shining upon the Earth. But he finds the problems of plane constructions such as the regular heptagon introduce some error and thus there is a sort of missing piece that must exist somewhere not on the plane, at least the plane as known to be defined of constructible points. Anything not on the plane must be in space or heaven above similar to the ideal forms of Plato. He knows that the doubling of the cube on the plane can also introduce error and thus finds its unsolvability also a property of space or heaven. But when the cube problem has been solved by a three dimensional earthly process he can only conclude that his vague understanding of unsolvability or impossibility is not an earthly phenomenon but a heavenly one, and thus beyond three space dimensions. However he can easily observe the idea of a line and intersection of two lines to define a plane, and because his tool has been the straight-edge, or line, he must thus see that one line is a single dimension whereas two lines make a second dimension and that when he erects the perpendicular to the plane he has used the straight-edge again whereby understanding the addition of one, a new dimension. Therefore he sees the addition of one to two as a transition towards three. Since he has come to the enlightened conclusion that the impossibility which seems conceptually the same thing in the polygon problem as the cube problem and of it not being of three dimensions, it must be three plus one, or four, and is thus led to the four dimensions. Here it is a four dimensional object that is not the plano-plane. He would think of the complete 4 dimensional space as heaven. The impossibility in the cube doubling, discovered to be in heaven, is something he has already identified in this 4th dimension with the existence of the New Jerusalem, Heaven on Earth, the Light shining down from a heavenly source, the Christ returning. He may not have been able to extrapolate beyond the fourth dimension until later. It is possible that his later contacts with angels would steer him in this direction, for having realized that the New Jerusalem was in the future by perceiving time as the 4th dimension in a way beyond just a measurement of motion he was anticipating Einstein in a sense by regarding time as integrally related not just by movement but a necessary part of the holistic and ultimately eschatological description of the world.^[18] This is fundamentally different than the plano-plane combination, it is a fourth dimension based upon a cube plus a first degree object. This is precisely the important equation of the Ars Magna.

Later commentaries on the work of Harriot and his algebraic representations of dimensional objects, such as the fourth denoted aaaa would point out the absurdity of the objects beyond three dimensions as being anything but imagination because to add a first degree object to a cube was, and in general even today, considered absurd. However, Booth writes that Harriot may have been able to take the conceptual leap, beyond the dimensional restrictions, but still requiring homogeneity for calculation, based upon his experience with the Native Americans whose language he translated.^[19] For the substantial difference was that this culture had a concept of a fourth person in their language something English and other European languages did not. This would have come as a conceptually challenging problem for Harriot to resolve and it is suggested that it could have really only become aware to Harriot fully by being developed into his later mathematical researches. Those researches were aided by his work on navigation which was dependent upon the emerging artistic concept of perspective, or projectivity.

To compare this with John Dee, when he wrote the Monas, he himself recognized he was extremely inspired by the voice of God. Thus in a very literal sense there was a fourth person, that in essence was there speaking, and not merely the more abstract God of the traditional Trinity. Together with that Trinity indeed there become four persons that Dee is recognizing. He would also readily point to the fact that the tetrahedron, the equidistributed solid according to the tradition of Plato, is to be identified with fire. This has already been emphasized in Theorem X that without the application of fire the process described by the Hieroglyph could not take place. He also states in Theorem XIII regarding its action that it cannot take place in this epoch unless complicated alchemical procedures are undertaken. This specifically references the futuristic view of this doubled cube. In Theorem XXIII he goes further to indicate the necessity of a time period of four super-celestial cycles. Without speculating on the interpretation of this it is clear this only adds to the temporal aspect of the dimension. Dee, having the same access to the concepts of perspective and projectivity again point to the far distance of the point as it is constructed. Today mathematically projective geometry can be described as taking a space and adding an extra dimension through the adjunction of a point at infinity. Dee would not have thought of it quite as technically as this but the potentials were there.

But he was also aware of the impossibility or unsolvability as some sort of object residing in heaven. If he recognized these "errors" in approximation as things residing in heaven, a divine place of perfection, then the errors must not be errors after all but some other type of object in the heavenly abode. Thus most likely his contemporaries would have seen these to be the stars. But his unique insight told him that they were beyond the stars in something higher than the firmament. One can only conclude that he must have thought of them as divine objects. But for the case in point and , there must be a similar sort of divine energy, that which he already identified as Christ, or LVX.

So he resolves back into the description of the glyph that it is the point that is necessary for the Binary to define the Ternary and ultimately the Quaternary. He has shifted the awareness to the 1, 2, 3, 4 sequence but now for those that could see he has illuminated a sequence of dimensions. If one turns attention to Theorem XII, the crucial lemma for XX, one may also observe his explanation of dimension there. In the second diagram of Theorem XII beginning with notice a rotation into and a reflection. This rotation is a one to two dimensional transformation. Next imagine raising both and into the z direction. After rotation, the analogue of the reflection, one is left with two arcs, the halves of the Aries sign, that define the lune. Next, upon letting the moon revolve around the earth, a process of time, one is left with the primitive Mercurial sign. Thus he has demonstrated clearly the results of 3 transformations and finally synthesized it into one sign, in the spirit realm, something that could in a sense be seen as a process orthogonal to all of the previous and thus defining a 5th dimension. One would speculate that his kabbalistic and Pythagorean notions with regard to the sum 1+2+3+4=10 that indicates completion, would probably put a boundary on his musings of any higher dimensions.

THEOREM XX

          We have shown sufficiently that for very good reasons the Elements are represented in our Hieroglyph by the straight lines, therefore we give a very exact speculation concerning the point which we place in the centre [focus, (also Christ)] of our Cross. This point cannot by any means be abstracted from our Ternary [cube]. Should anyone who is ignorant of this divine learning, say that in this position of our Binary [duplication process] the point [focus] can be absent, we reply, he may suppose it to be absent, but that which remains without it will certainly not be our Binary [duplication process with a necessary focus for the conic construction]; for the Quaternary [successfully duplicated cube] is immediately manifested, because by removing the point we discontinue the unity of the lines. Now, our adversary may suppose that by this argument we have reconstructed our Binary [merely the duplication process]; that in fact our Binary [duplication] and our Quaternary [duplicated] are one and the same thing, according to this consideration, which is manifestly impossible. The point [focus] must of necessity be present, because with the Binary [duplication] it constitutes our Ternary [projecting cube], and there is nothing that can be substituted in its place. Meanwhile he cannot divide the hypostatic property of our Binary without nullifying an integral part of it [the transcendental nature of the "Christ" focus, that which makes for a successful duplication]. Thus it is demonstrated that it must not be divided. All the parts of a line are lines [inherent connectivity, (see Theorem II & VII)]. This is a point, and this confirms our hypothesis. Therefore, the point does not form part [separable object] of our Binary [duplication] and yet it forms part of the integral form [active principle] of the Binary [duplication process]. It follows that we must take notice of all that is hidden within this hypostatic form and understand that there is nothing superfluous in the linear dimension [projective quality] of our Binary [duplication]. But because we see that these dimensions are common to both lines, they are considered to receive a certain secret image from this Binary. By this we demonstrate here that the Quaternary [duplicated] is concealed within the Ternary [the cube]. [The amazing moment of enlightenment comes from mentally comprehending the mathematically essentially transcendental impossibility of this construction!] O God! pardon me if I have sinned against Thy Majesty in revealing such a great mystery in my writings which all may read, but I believe that only those who are truly worthy will understand.

This analysis has been for the most part one based purely at a mathematical level with only the inclusion of naive biblical prophecy and meaning. It thus invites an exploration of the more abstract metaphysical connotations that would arise from considering it as an alchemical transformation process. To this end the study of the kabbalistic correspondences pertaining to the significance of the Moon, the Sun, and Elements, and the relationship with the composite glyph of Mercury, is necessary. This notion of the fourth dimension in Dee’s work is not new. The theory proposed by Bridges and Burns is that prior to the writing of the Monas, relating aspects of the Olympic Sprits, by connecting metaphysical correspondences geometrically in the structure of two cubes into a composite structure Dee was able to comprehend an object of 4-dimensional character, that of the hypercube.^[20] Further, Burns and Moore reveal the existence of the conic sections already occurring in Theorem XVI. One of the implications of this appearance of a cone is in the proposition put forth that indeed such a cone can be indicative of the precession of the equinoxes.^[21] If the space constructed by the process of duplication of the cube is indeed representative of the New Jerusalem cube of space and the cone is a unique one also in correspondence with the precession cone, then the critical point of construction , the non-constructible number, would indeed be a temporal critical point. It is presently obvious that a major critical point of the precessional cycle, is one found at the completion or beginning of a cycle. It is commonly held that the Mayan calendar marks this point and it coincides with the year 2012.^[22]

This leaves several natural questions. If this is neither constructible nor transcendental may it be determined by a process intermediate to these concepts, an alchemical process? If yes, and that alchemically constructed point is formed in conjunction with the precessional cone what type of process must occur for that critical point to exist in something more than just a theoretical sense? What objects must conjoin? Dee uses and and Burns discusses the apocalyptic implications of the conjunctive cycles of and in Dee’s lifetime including the so-called "Fiery Trigon" 20 years after he completed the Monas.[^23] Is there a conjunction of planets, in the neighborhood of 2012, which is relevant? Is there significance related to the perceived motion being similar to a solar eclipse? These questions and many more seem to fall in the realm of global alchemy. What is to be said of local personal alchemy? The answers to these questions may shed light on any perceived context on the Enochian corpus then as it unfolded to Dee during that time of the "Fiery Trigon" and the modern resurgence of interest combined with the modern day knowledge of the precessional cycle.

From a more mathematical perspective is the fact of the Solar glyph, the site of the original focus, represented by a circle significant to the effect of being "squared" as a result of the cubing process? Is this then, not merely a circle but a sphere? If the liberty of utilizing modern mathematical concepts in interpretation is allowed, similar to a language decoding or translation process, together with a supposition that John Dee was not merely in communicative contact with Ophanic intelligences in later life but that his entire life had been a series of contacts only with a culmination in the actual angelic conferences, what modern concepts may be used to facilitate a better understanding and application of the Enochian material? For instance can this entire object, the sun glyph, actually be a higher dimensional sphere, of much larger that three or four dimensions? When his frontispiece states "Mercury becomes parent and the king of all planets when perfected by stable, pointed Stilbon" and Stilbon is also another aspect of Mercury emphasizing the scripting and communicative aspect, then would this then not form a core or essence of Mercury and a Mercurial action, astrologically modernized to a communication device?^[24]

1 J. L. Heilbron, Introductory Essay to John Dee in Astronomy (Berkeley, CA: University of California Press, 1978), p. 25.

2. Viète’s maxim was "To Solve Every Problem" see François Viète, The Analytic Art (Kent, OH: The Kent State University Press, 1983), p. 32.

3. Mathematics is the subject matter of the entire second book, that begins with the chapter heading "Of the necessity of mathematical learning, and of the many wonderful works which are done by mathematical arts only." Henry Cornelius Agrippa, Three Books of Occult Philosophy, (St. Paul, MN: Llewellyn Publications, 2003), p. 233.

4. "Chapter XI: On the Cube and First Power Equal to the Number" in Girolamo Cardano, The Great Art or the Rules of Algebra (Cambridge, MA: The M.I.T. Press, 1968), p. 96.

5. Michael Booth, "Thomas Harriot's Translations," The Yale Journal of Criticism 16, no. 2 (2003): 346.

6. Viète titles his Chapter III of the Introduction to the Analytic Art, "On the Law of Homogeneous Terms and on the Grades and the Kinds of Magnitudes of Comparison. The axiom is stated thus, "homogeneous terms must be compared with homogeneous terms," The Analytic Art, p. 15.

7. Ibid., p. 16.

8. Max Jammer, Concepts of Space (New York: Dover Publications, 1993), p. 58.

9. For example a thorough discussion may be found in Chapter XXVI, "The Rise of Abstract Algebra" in Carl B. Boyer, A History of Mathematics (Princeton, NJ: Princeton University Press, 1985), p.620-648.

10. Wantzel, L. "Reserches sur les moyens de reconnaître si un Problème de Géométrie peut se résourdre avec la règle et le compas." Journal de Mathématiques Pures et Appliquées 1, no. 2 (1837): 369-370.

11. For a general overview consult Felix Klein, Famous Problems of Elementary Geometry (New York: Dover Publications, 1956). Technical details may be found in Jesper Lützen, Joseph Liouville 1809-1882 : Master of Pure and Applied Mathematics (New York: Springer-Verlag, 1990).

12. Julian Lowell Coolidge, A History of the Conic Sections and Quadric Surfaces (Oxford: Oxford University Press, 1945), p.13.

13. Ibid., p. 26.

14. Werner was acquired in April, 1550. For information on Dee’s holdings see John Dee, John Dee's Library Catalog (London: Bibliographical Society, 1990).

15. Coolidge, Conic Sections, p.1.

16. Agrippa and Dee view this as elementary, celestial and intellectual, or terrestrial, astrological, and spiritual, and the Three Books of Occult Philosophy are focused accordingly, Agrippa, p. 3..

17. Revelations Chapter 21, Verse 1, "And I saw a new heaven and a new earth: for the first heaven and the first earth were passed away; and there was no more sea," King James Bible.

18. Of course Einstein went much further than any of this by pointing to the dependency between space and forces acting over time as a type of 4-dimensional geometric object space-time, where the relations are not simple rather they are described by Einstein's field equations. see for instance Max Jammer, Concepts of Space (New York: Dover Publications, 1993).

19. Michael Booth, "Thomas Harriot's Translations," p. 357.

20. Vincent Bridges, and Teresa Burns, "The Little Book of Black Venus - Part Two: Olympic Spirits, the Cult of the Dark Goddess, and the Seal of Ameth," Journal of the Western Mystery Tradition 13, no. 2 (2007): §6.

21. Teresa Burns, and J. Alan Moore, "The Hieroglyphic Monad of John Dee, Theorems I-XVII: A Guide to the Outer Mysteries," Journal of the Western Mystery Tradition 13, no. 2 (2007).

22. Jay Weidner, and Vincent Bridges, The Mysteries of the Great Cross of Hendaye: Alchemy and the End of Time (Rochester, VT: Destiny Books, 2003).

23. Teresa Burns, "The Little Book of Black Venus and the Three-Fold Transformation of Hermetic Astrology," Journal of the Western Mystery Tradition 12, no. 2 (2007).

24. See the section "The Frontispiece" of Burns and Moore.